Precision lenses do an excellent job conveying contrast and color from object to image, but they can do a poor job of transferring accurate dimensions, especially if they have small focal lengths. Traditional lenses work in the same way as the human eye: nearer objects appear larger than farther objects. This change in magnification with respect to distance is partially what allows for depth perception, but it will reduce the accuracy of a machine vision system that is being used for precise measurements. If a vision system requires the most accurate possible measurement, it is imperative to ensure that the relationship between an object’s dimensions and the corresponding image’s dimensions is well-defined and unchanging. For these systems telecentric lenses are required.

Telecentric Lenses

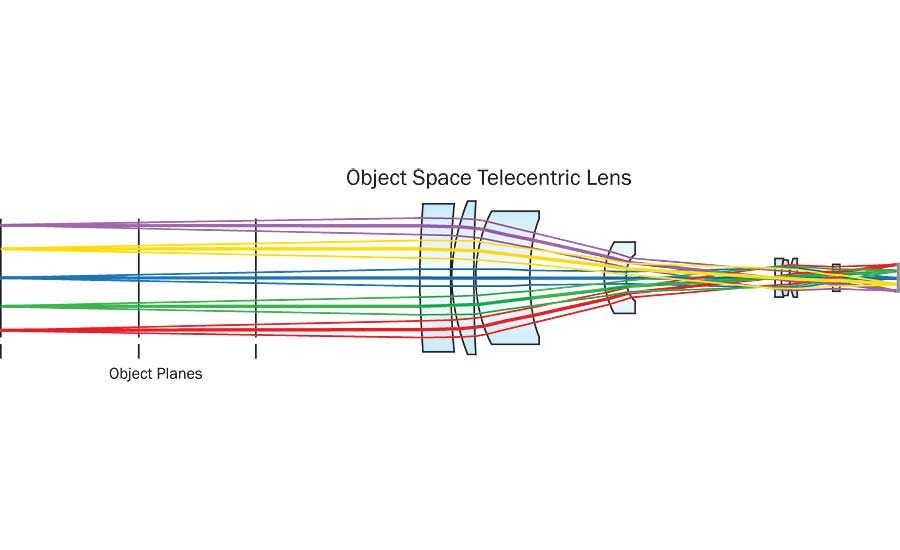
Optically, a telecentric lens is defined as a lens in which the chief rays are parallel to the optical axis. That property has some interesting corollaries. Chief rays in a telecentric lens will be normal to the object plane, the image plane, or both; and the entrance pupil and/or the exit pupil is located at their respective infinities. The field of view of a telecentric lens is non-angular, meaning it doesn’t change size with distance from the lens. Finally, and most importantly for machine vision applications, magnification in a telecentric lens is independent of object distance. It is important to note that these are not unrelated properties, but are traits that all telecentric lenses have.

There are three different types of telecentric lenses, each of which have distinct properties. When a lens is referred to as simply a telecentric lens, it is most likely an object-space telecentric lens. Object-space telecentric lenses have their entrance pupil located at infinity in object space, which means the chief rays in object space are parallel to the optical axis (Figure 1).

Image-space telecentric lenses are the opposite: they have their exit pupil at infinity in image space and the rays in image space are parallel to the optical axis; meaning that the chief rays are normal to the image plane (Figure 2).

When both object-space and image-space telecentricity are incorporated into a single lens it becomes a bi-telecentric lens, also called a doubly telecentric lens (Figure 3).

The Benefits of Object-Space Telecentricity

An object-space telecentric lens only transmits chief rays that are perpendicular (or nearly perpendicular) to the entrance pupil. If two features of an object are separated by 12 mm, the rays the telecentric lens accepts retain that 12 mm separation all the way to the objective lens (scaling by the lens’s magnification). The position of the incoming ray from a given object feature remains the same regardless of the distance the lens is from the object. For example, the chief rays from the features separated by 12 mm are imaged by a .067X magnification telecentric lens at a distance separated by 800 µm on the detector — no matter the object distance. The invariability of magnification with object distance is independent of the depth of field, which is a function of f/#. Images created by a telecentric lens, just as those from a traditional lens, will increasingly blur as the object distance varies from optimum working distance; however, a telecentric lens makes it appear as if everything within the depth of field is at the same object distance.

Traditional fixed focal length lenses suffer from distortion: a change in magnification across the field. In the presence of distortion, the apparent size of an object varies with its position in the field of view. Telecentric lenses typically have much lower distortion than traditional lenses, such that the size of an image produced by a telecentric lens remains constant as the object distance and its position in the field vary (Figure 4).

This magnification invariance is where the object-space telecentric lens shows its value for metrology. Take, for example, the task of measuring the dimensions of parts as they pass by on a conveyor belt. Unless the placement is perfectly repeatable and the synchronization between camera and conveyor is equally perfect, each successive object will be imaged at a slightly different location in the field. In addition, products on the conveyor slightly undulate with the movement of the conveyor, putting each at a different distance from the lens. Both of these effects reduce the accuracy of any metrology done with a fixed focal length or a zoom lens, while a telecentric imaging lens will produce the same image even with these effects present.

Object-space telecentric lenses are also valuable for such activities as pick-and-place operations. A circuit board, for example, presents a three-dimensional scene. With a fixed focal length lens, parallax error can obscure more distant features behind nearer surfaces of components already placed on the board. The image created by a telecentric lens doesn’t suffer from parallax error; each position on the circuit board is imaged as if observed from directly above.

The Benefits of Image-Space Telecentricity

Image-space telecentricity has a corresponding set of characteristics. In the same way that magnification in an object-space telecentric lens does not change with object distance, magnification in image-space telecentric lenses does not change as the sensor shifts from its optimal position. This reduces fabrication and placement tolerance on the sensor, and leads to an even more accurate measurement.

 Another significant implication of the chief rays being normal to the image plane is that image-space telecentric lenses have uniform illumination across the field. Illumination across the image plane of a fixed focal length lens falls off as the 4th power of the cosine of the ray angle (cos⁴) relative to the optical axis. Since the angle is theoretically 0degrees and does not vary in an image-space telecentric lens, the illumination does not roll off and relative illumination remains at 100% across the full field. The lack of variation in incident angle also optimizes the performance of sensors that incorporate un-shifted microlenses to increase the effective fill factor. Microlenses are effective only for a relatively small angle of incidence, which is guaranteed all across the image sensor with an image-space telecentric lens.

Telecentric = Perfect?

A doubly telecentric lens is both image-space and object-space telecentric and, as might be expected, combines the features of both types of telecentricity. The field of view in a doubly telecentric lens is completely unaffected by change due to shifts in the object position or the sensor position, and they do not suffer from any cos⁴roll-off.

Another positive implication of double telecentricity is that the blur caused by defocus is symmetric. That is, as the object distance shifts out of the nominal depth of field, there’s no shift in the centroid of the image of the spot associated with a point on the object. In fact, there are some applications in which it may be advantageous to defocus an image to provide a more accurate determination of edge position in order to avoid sub-pixel interpolation — which can’t be done as accurately with the asymmetric blur of traditional fixed focal length lenses. Considering all of these advantages, telecentric lenses can seem unbeatable for many machine vision applications.

In practice, no telecentric lens is perfect. That is, no telecentric lens images only light entering parallel to the optical axis. A telecentric lens may be characterized by its degree of telecentricity, or simply telecentricity, which is the deviation of the principal ray from parallelism to the optical axis. Telecentricity is typically measured in degrees. So, for example, a lens with an object-space telecentricity of 0.3 degrees will accept light at angles of up to 0.3 degrees away from parallel to the optical axis. When telecentricity is examined in more detail, it can be found that it varies with field position and wavelength as well. The small residual distortion also varies across the field, in many cases non-monotonically. But due to the typically small amounts of distortion, it can be calibrated out quite easily for applications that demand the highest accuracy.

Even if all imperfections could be avoided, telecentric lenses have some characteristics that make them unsuitable for every application. First, the field of view of an object-space telecentric lens cannot exceed the size of the objective lens — so it cannot be used to image anything larger than the objective. This means that they are generally larger than an equivalent fixed focal length lens, which is a direct consequence of the fact that they have no angular field of view.  Likewise, the image sensor dimensions in an image-space telecentric lens cannot exceed the size of the back of the lens. As the size of the lens increases, so does the weight, and so does the cost.

 Still, the high accuracy inherent in telecentric lenses is often the most cost-effective way to solve a measurement problem. It is easy to get lost in the details of telecentric lens design, so one of the best ways to ensure proper lens selection for any application is to choose a vendor who has a range of standard telecentric lenses to choose from and the ability to produce custom designs. Take the time to discuss your application with your manufacturing partner, as proper lens selection will pay dividends far greater than the initial investment.